List of map projections
This list sorts map projections by surface type. Traditionally, there are three categories by which projections are sorted: cylindrical, conic and azimuthal. As a result of the complexity of projecting great circles onto flat planes, most do not fit perfectly into one category. Alternatively, projections may be classified by the properties which they preserve namely: direction, localized shape, area and distance.
Projections by surface
Cylindrical
The term "cylindrical projection" is used to refer to any projection in which meridians are mapped to equally spaced vertical lines and circles of latitude (parallels) are mapped to horizontal lines (or, mutatis mutandis, more generally, radial lines from a fixed point are mapped to equally spaced parallel lines and concentric circles around it are mapped to perpendicular lines).
Pseudocylindrical
Pseudocylindrical projections represent the central meridian and each parallel as a single straight line segment, but not the other meridians. Each pseudocylindrical projection represents a point on the Earth along the straight line representing its parallel, at a distance which is a function of its difference in longitude from the central meridian.
Conical
Azimuthal projections have the property that directions from a central point are preserved (and hence, great circles through the central point are represented by straight lines on the map). Usually these projections also have radial symmetry in the scales and hence in the distortions: map distances from the central point are computed by a function r(d) of the true distance d, independent of the angle; correspondingly, circles with the central point as center are mapped into circles which have as center the central point on the map.
Pseudoconical
Azimuthal
Pseudoazimuthal
Polyhedral maps
Main article:
geodesic gridPolyhedral maps can be folded up into a polyhedral approximation to the sphere. Many polyhedral maps use a gnomonic projection for each face, but some cartographers prefer the Fisher/Snyder equal-area projection for each face or a conformal projection.[1]
Projections by preservation of a metric property
Conformal
Equal-area
Hybrids that use one equal-area projection in some regions and a different equal-area projection in other regions are almost always designed to be equal-area as a whole, such as:
- HEALPix: Collignon + Lambert cylindrical equal-area
- Goode homolosine: sinusoidal + Mollweide
- Philbrick Sinu-Mollweide: sinusoidal + Mollweide, oblique, interrupted.
- Hatano asymmetric: two different pseudocylindric equal-area projections fused at the equator.
Equal-area polyhedral maps typically use Irving Fisher's equal-area projection, whereas most polyhedral maps use the (non-equal-area) gnomonic projection.[4]
Equidistant
Equidistant projections preserve distance from some standard point or line.
- Azimuthal equidistant—distances along great circles radiating from centre are conserved
- Equirectangular—distances along meridians are conserved
- Plate carrée—an equirectangular projection centered at the equator
- Cassini — a transverse aspect of the Plate carrée centered on some selected meridian. Also called Soldner projection or Cassini–Soldner, particularly in ellipsoidal form.
- Equidistant conic—distances along meridians are conserved, as is distance along one or two standard parallels[5]
- Werner cordiform distances from the North Pole are correct as are the curved distance on parallels
- Two-point equidistant: two "control points" are arbitrarily chosen by the map maker. The two straight-line distances from any point on the map to the two control points are correct.
- orthographic preserves distances along parallels.
- Sinusoidal—distances along parallels are conserved
- Lambert azimuthal equal-area—the straight-line distance between the central point on the map to any other map is the same as the straight-line 3D distance through the globe between the corresponding two points.
- American polyconic—distances along the parallels are preserved; as is distance along the central meridian.
Gnomonic
| Projection |
Images |
Creator |
Notes |
| Gnomonic |
|
|
Retroazimuthal
Compromise projections
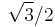 .
.